Les astronomes résolvent le mystère de l’origine du calendrier chinois ?

Un calcul informatique basé sur les éphémérides n’a donné qu’une seule correspondance possible : le 5 mars 1953 avant JC. 

A l’aube de ce jour, Mercure, Vénus, Mars, Jupiter et Saturne se sont alignés comme un collier de perles dans le ciel oriental, à côté du “grand carré de Pégase”.  

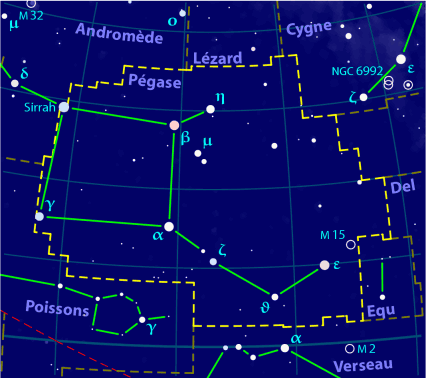
Pégase est une constellation de l’hémisphère nord, située au sud d’Andromède, au nord des Poissons et au nord-ouest du Verseau.

La constellation se dessine à partir du Grand carré de Pégase. 

Les trois étoiles les plus brillantes de Pégase forment, avec α And (ou Alpheratz, ou Sirrah), un astérisme appelé le « Carré de Pégase », caractéristique de la constellation. 

Le grand carré est un repère majeur de la voûte céleste, qui se reconnaît directement à sa forme, et à l’absence d’étoile significative à l’intérieur. 

Cette constellation est remarquable pour visualiser le quadrillage de la voûte céleste : le bord « gauche » du carré marque le méridien origine (qui passe par le point gamma, intersection de l’équateur céleste et de l’écliptique).

L’écart entre deux bords « verticaux » est de 15 degrés, ce qui permet de visualiser le déplacement angulaire de la voûte céleste en 1 h. 

Les deux bords « horizontaux » sont à 15° et 30°N, ce qui permet de situer l’équateur céleste.

C’est dans ce carré de Pégase que le 5 mars 1953 avant JC, les planètes s’étalent toutes sur quelques degrés. 

La nouvelle lune se produit peu de temps après lorsque le soleil, la lune et cinq planètes se trouvent tous alignés dans Pégase, exactement comme Liu l’avait écrit. 

Cette date marque donc en effet le début des cycle planétaires, du comptage des jours, des mois, des années, le moment magique recherché par les astronomes chinois et les jésuites pendant plus de 2000 ans.

Pour mieux comprendre l’importance fondamentale de ces mouvements ou oscillations cycliques des corps célestes je vous propose d’abord une expérience de physique très connue qui consiste à observer les mouvements une série de pendules possédant des périodes d’oscillations croissantes.

Lorsqu’ils sont simultanément libérés, ils produisent l’effet d’une onde transversale changeante qui revient aux conditions de départ après un certain temps. 

Les longueurs de chaque pendule sont liées à celle qui lui est adjacente de telle sorte qu’après un certain nombre de balancements, les pendules sont de nouveau en phase.

Pour calculer les longueurs des pendules, commencer par la période la plus longue, T .

Décidez du nombre de cycles de ce pendule que vous souhaitez observer, avant que tous les pendules ne soient de nouveau en phase. 

Si par exemple nous utilisons 16 cycles, cela signifie que la période d’oscillation du prochain pendule ( T a ) doit être telle qu’il faudra 17 cycles pour être en phase avec le premier, le suivant prendra 18 cycles, le suivant 19, etc…

Cela conduit aux relations : 16T = 17 T a , 16T = 18 T b et 16T = 19 T c, etc.

Pour calculer les longueurs des pendules , formez le rapport des périodes en fonction des longueurs, puis résolvez le rapport des longueurs en fonction des périodes. 

Le résultat montre que la longueur que vous recherchez est la longueur du pendule le plus long multipliée par le carré du rapport des périodes de temps au carré. 

Par exemple: L a = L (16/17) 2 , L b = L (16/18) 2 , L c = L (16/19) 2 , etc….où L est la longueur du pendule le plus long . 

Lorsque vous décidez de la longueur souhaitée du pendule le plus long, les longueurs des autres peuvent être calculées facilement.